AS Physics¶

Practical Equipment¶

Momentum¶

The product of mass and velocity.

$p = mv$

The Principle of Conservation of Momentum¶

The total linear momentum before a collision is equal to the total linear momentum after a collision unless the system is acted on by a resultant external force

Force¶

The rate of change of momentum

$F = \dfrac{\Delta p}{\Delta t}$

Collisions¶

Elastic Collisions¶

The collision in which the total kinetic energy of the system is conserved

• The relative speed of approach = the relative speed of separation

Inelastic Collisions¶

The collision in which the total kinetic energy is not conserved

• Occurs when objects crumple and deform

Center of Gravity¶

The point at which the weight of the object may be considered to act

Moment¶

The turning effect of a force

$moment = Fd$

Couple¶

A pair of forces that acts to produce rotation only

• Equal in magnitude
• Opposite in direction
• Perpendicular to the distance between them

Torque¶

The moment of a couple

$\tau = Fd$

The Principle of Moments¶

For a system to be in equilibrium, the sum of clockwise moments about a point must be equal to the sum of the anticlockwise moments (about the same point)

Archimedes' Principle¶

An object submerged in a fluid at rest has an upward buoyancy force (upthrust) equal to the weight of the fluid displaced by the object

$F = \rho g V$

Energy¶

The Principle of Conservation of Energy¶

Energy cannot be created or destroyed, it can only be transferred from one energy store to another

Gravitational Energy¶

Energy stored in a mass due to its position in a uniform gravitational field

Kinetic Energy¶

Energy an object has due to its motion

Deformation¶

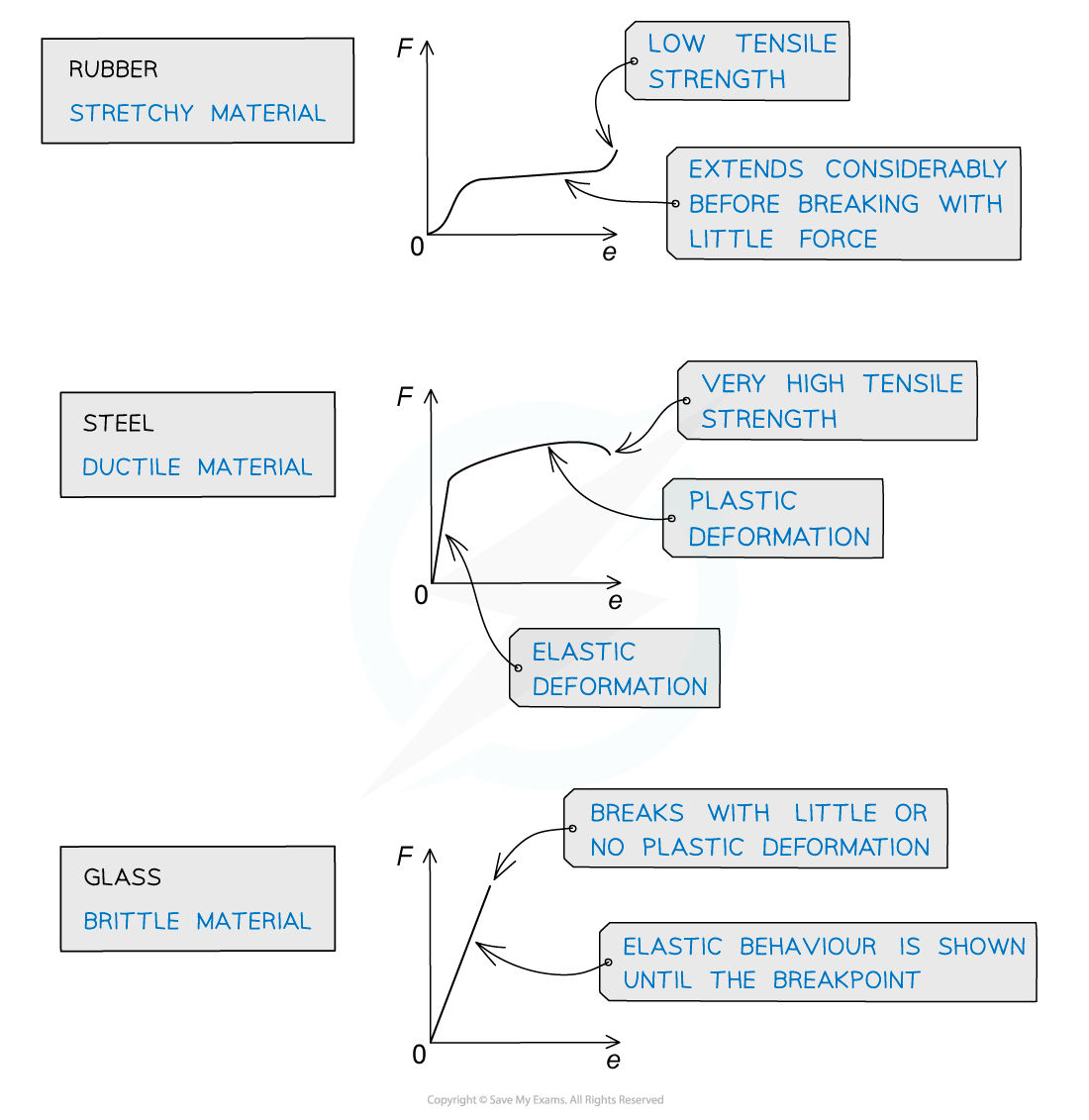
Hooke's Law¶

Extension is directly proportional to the applied force

$F = kx$

The Spring Constant¶

A measure of the stiffness of a spring

$k = \dfrac FX$

Stress¶

Applied force per unit cross sectional area

• The ultimate tensile stress is the maximum tensile stress before breaking

$\sigma = \dfrac FA$

Strain¶

Extension per unit length

$\epsilon = \dfrac XL$

Young Modulus¶

The ratio of stress and strain

• A measure of how stiff or elastic a material

$E = \dfrac \sigma \epsilon = \dfrac{FL}{Ax}$

Wave¶

The Wave Equation¶

$v = f \lambda$

Wave Intensity¶

$I = \dfrac PA$

$I \propto A^2$

$I \propto f^2$

Progressive Waves¶

Waves that transfer energy without transfer of matter

Transverse Waves¶

A wave in which the particles oscillate perpendicular to the direction of motion and energy

• Peaks and troughs
• Electromagnetic waves, visible light, UV, vibrations on strings
• Can be polarized

Longitudinal Waves¶

A wave in which the particles oscillate parallel to the direction of motion and energy transfer

• A rarefaction is an area of low pressure, with the particles being further apart from each other
• A compression is an area of high pressure, with the particles being closer to each other
• Cannot travel through a vacuum
• Sound waves

Doppler Effect¶

$f_o = f_s (\dfrac{v}{v \pm v_S})$

• $v$: wave velocity

• $v_s$: velocity of the source relative to the observer

• Source moving towards: $v - v_s$

• Source moving away: $v + v_s$

• Source is moving

• Observer is stationary

Electromagnetic Spectrum¶

• Memorization:
  • 1 4 1 4 7 1 1
  • 6 3 8 7 7 3 1

Malus's Law¶

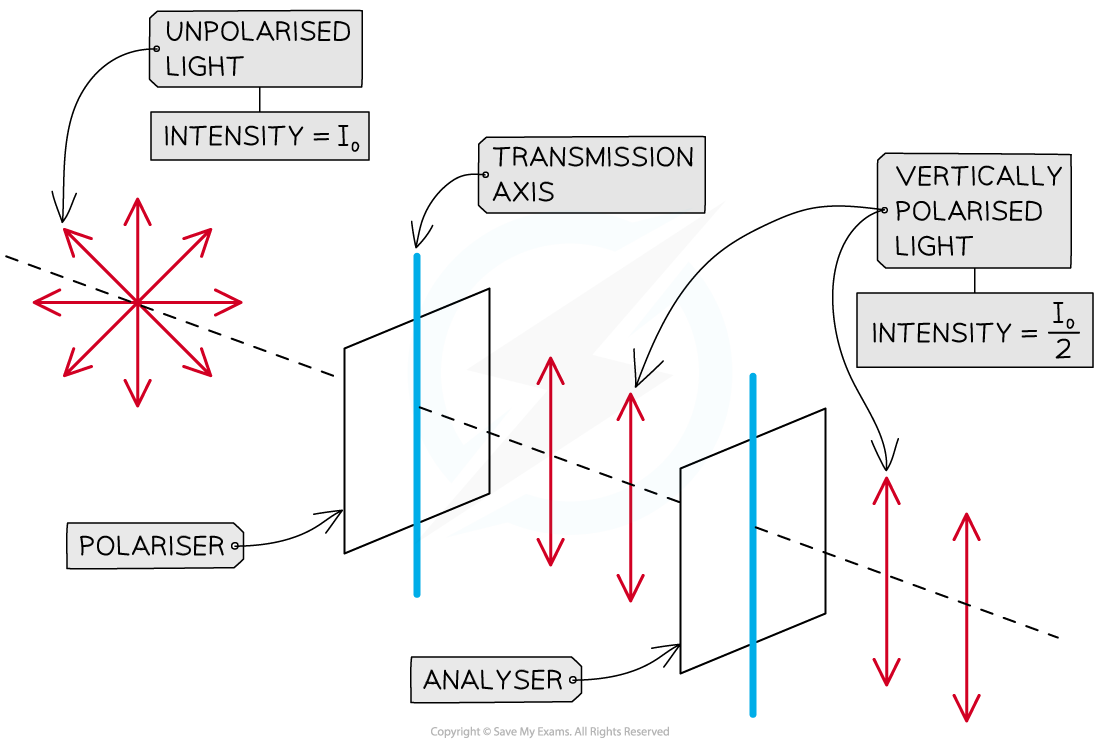
If unpolarized electromagnetic waves of intensity $I_0$ pass through a polarizer, the intensity of the transmitted polarized waves falls by a half

$I = \dfrac{I_0}2$

If the analyzer is rotated by an angle θ with respect to the polarizer, the intensity of the waves transmitted by the analyzer is given by the equation

$I = I_0 \cos^2(\theta)$

Superposition¶

The Principle of Superposition¶

When two or more waves overlap at a point, the displacement at that point is equal to the sum of the displacements of the individual waves

Wavelength of Stationary Waves¶

Waves that do not transfer energy and matter

Fundamental Mode of Vibration / First Harmonic¶

The simplest wave pattern of a wave fixed at both ends is a single loop made up two nodes and an antinode.

• Nodes are locations of zero amplitude
• Antinodes are locations of maximum amplitude

Zero Open Ends¶

$L = \dfrac{n \lambda}2, n \in [1, 3]$

One Open End¶

$L = \dfrac{n \lambda}{4}, n\ is\ odd$

Two Open Ends¶

$L = \dfrac{n \lambda}2, n \in \mathbb{N}^*$

Diffraction¶

The spreading out of waves when they pass an obstruction

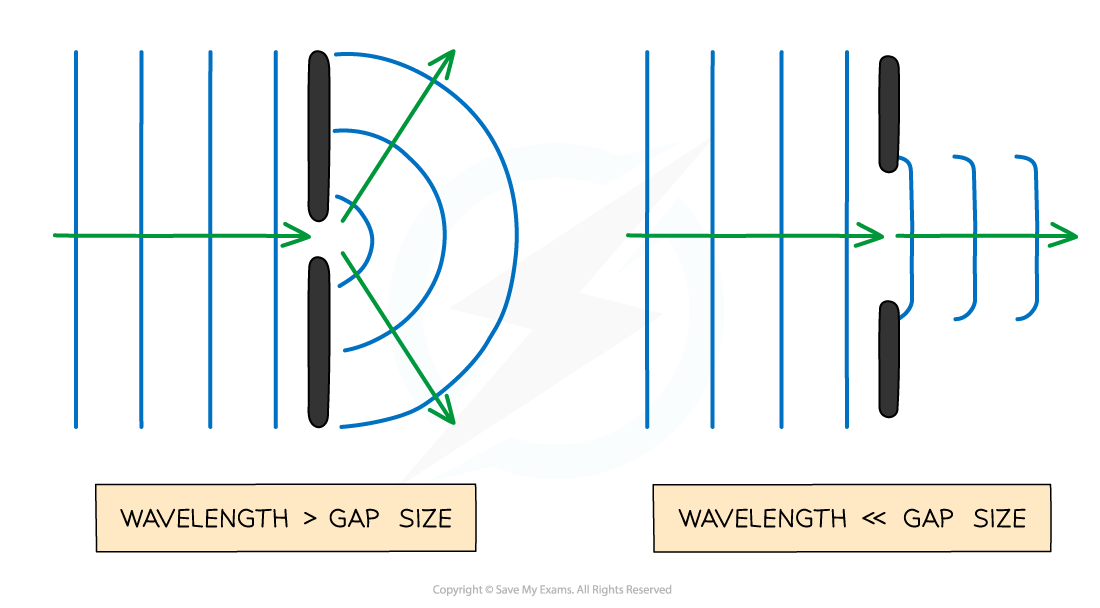
Conditions for Constructive & Destructive Interference¶

• Constructive interference: path difference = $n \lambda, n \in \mathbb{N}$
• Destructive interference: path difference = $(n+\dfrac12) \lambda, n \in \mathbb{N}$

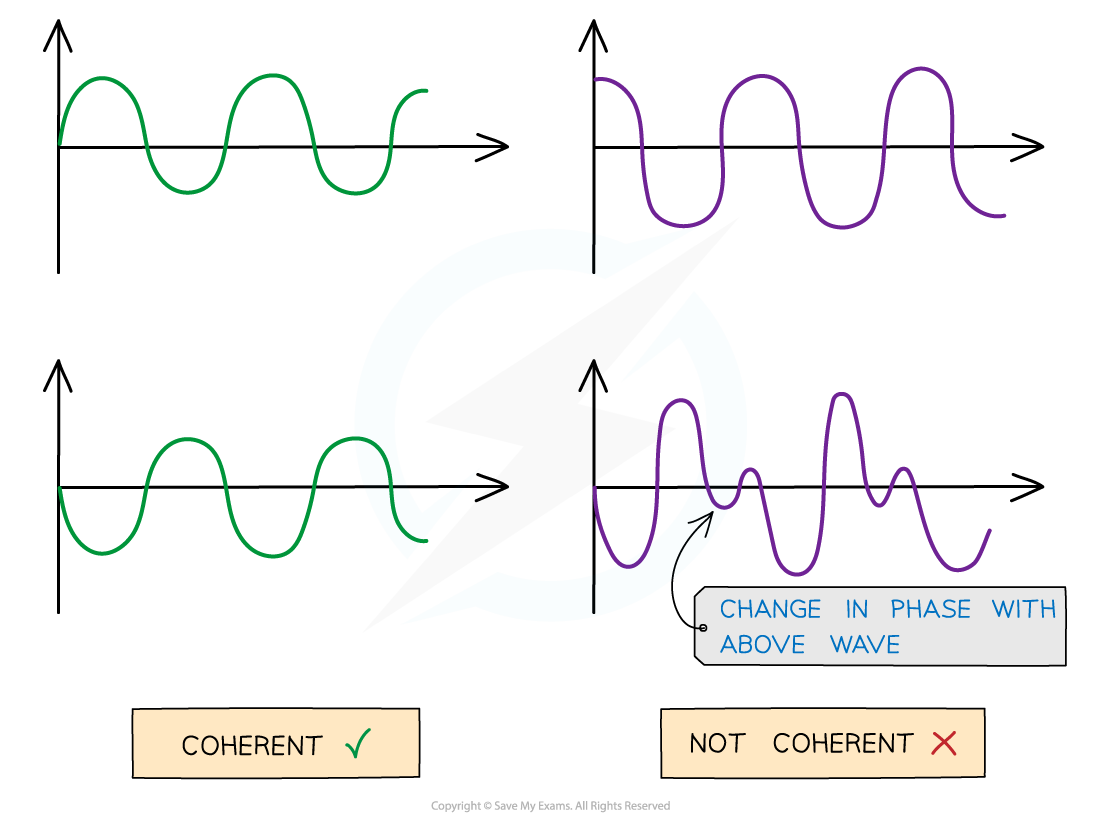
Coherence¶

Waves have the same frequency and constant phase difference

Double Slit¶

$\lambda = \dfrac{ax}D$

• $\lambda$: wave length of source
• $a$: distance between the centers of the slit
• $x$: fringe width (distance between successive bright fringes)
• $D$: distance between the slits and the screen

The Diffraction Grating¶

• Use monochromatic light: one wavelength
• From a laser to ensure that the light beams are coherent
• Better than Young's double slit

$a \sin(\theta) = n \lambda$

• $a$: spacing between adjacent silts
• $\theta$: angular separation between the order of maxima
• $n \in \mathbb{N}$: order or maxima
• $\lambda$: wavelength of source

To calculate the orders of maxima, $\theta = 90^\circ, \sin(\theta) = 1$

Silt Spacing¶

Diffraction gratings come in different sizes measured by lines/m, represented by $N$

$d = \dfrac1N$

Atomic Structure and Particle Physics¶

Nuclear Force¶

Strong Nuclear Force: A fundamental force that acts between particles such as protons and neutrons, but which does not affect particles like electrons

Radiation¶

• $\alpha: ^A_Z X \rightarrow ^{A-4}_{Z-2}Y + ^4_2 \alpha$
• $\beta^-: n \rightarrow p + ^0_{-1}\beta^- + \overline{v_e}$
• $\beta^+: p \rightarrow n + ^0_{+1}\beta^+ + v_e$

Particles¶

Leptons: subatomic fundamental particles that are not affected by strong nuclear force

Hadrons: subatomic particles made up of quarks that are affected by strong nuclear force

Baryon: three quarks

Meson: one quark and one antiquark